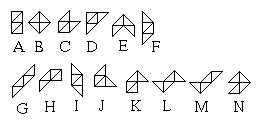
TRIMINI
The figure below show the 14 pieces that can be made composing four triangles.
The six pieces on the top row are symmetric, ie, coincide with teir mirror images.
Those on the bottom line are asymmetric.
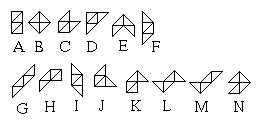
Overall the 14 pieces contain 56 triangles, therefore they could nicely fit on
the 4x7 rectangular board:
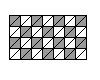
Unfortunately, this is not so !
Can you prove that it is not possible to arrange the 14 triminis on the 4x7 board?
Give this problem a try before continuing reading.
You may cut the trimini pieces out of a piece of cardboard and play with them.
The pieces A, B, C, D, E, F, G, I, J, L, M, and N always cover two black triangles and
two white triangles. There remain the odd pieces H and K which cover three triangles of
one color and
one of the other.
If the odd pieces (H and K) were in odd number we would be done.
Unfortunately they are in even number.
So this approach does not lead us to a proof
of impossibility of the cover.

In this coloring the pieces A, B, C, E, G, H, I, L always have one unit square black
and one unit white.
The pieces, F, J, K, M, and N, have 3/4 units of one color
and 5/4 of the other.
Finally the piece D can be either one unit black and one white,
or 3/2 one color
and 1/2 the other.
Counting the color units we have that one of the two equations must have an integer
solution for the covering to be possible:
8 * 1 + x * 0.75 + (1-x) * 1.25 + 1 = 8 * 1 + (1-x) * 0.75 + x * 1.25 + 1 8 * 1 + x * 0.75 + (1-x) * 1.25 + 1.5 = 8 * 1 + (1-x) * 0.75 + x * 1.25 + 0.5
This proves that the 4x7 rectagle covering is not possible.
Marco Corvi - 2014