SUPPORT VECTOR MACHINE
C.J.C. Burges, "A tutorial on Support Vector Machines for pattern
recognition", Kluvier (???) p. 1-43
The theory of SVM arises from the question "Under what conditions, and how
fast, does the empirical mean converges uniformly to the true mean?".
Suppose to have n
observation pairs, (xi, yi).
Assume that these are drawn independently from the same probability
distribution P, ie, they are "iid". Ther task is to find a machine
that learns the association x->y.
Such a machine is described by a generic function f(x, a), where
a denotes the parameters of the machine that are to be determined
during the training. For example, a might be the weights of a
neural network.
Risk and VC dimension
The expectation of the test error (called "risk") is
R(a) = Int 1/2 | y - f(x,a) | dP(x,y)
The empirical risk is the measured mean error rate, over the training set,
ie, over the observation pairs.
In a binary pattern recognition problem y can have two values,
+1 or -1, and the loss (1/2)|y-f(x,a)| can be either 0 or 1.
The following bound holds on the risk, with probability 1-u,
R(a) ≤ Remp(a) + [(h(1+log(2N/h))-log(u/4))/N]1/2
where h is a non-negative integer, called the Vapnik-Chervonenkis
dimension of the data.
This results gives a method for choosing the machine that minimizes the
right hand side bound on the risk (for a fixed sufficiently small u).
Remark. For a set of functions {f(a)} the VC dimension dVC
is defined as the
maximum number of points that can be "shattered" by functions in the set, ie,
such that for any binary class assignment of the points there is a function
in the set which separates the points of the two classes.
Note that this is not to say that any set of dVC
points can be shattered.
The VC dimension is an index of the capacity of the set of functions.
For example the K nearest neighbor classifier (with K=1) has infinite VC
dimension, and zero empirical risk. The K-nn classifier performs well.
Linear Support Vector Machines
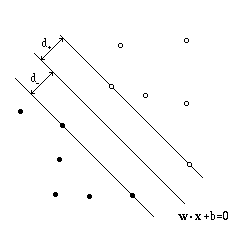 Supose that the set of training points are linearly separable, ie, there
exists a plane wx+b=0 such that the points
xi with yi=1 ("positive" points)
lay on one side and those with yi=-1 ("negative" points)
on the other side.
w is the normal to the plane and
|b|/|w| is the distance of the origin from the plane.
Let d+ and d- be the shortest distances of the
positive and negative points, respectively, from the separating plane.
The margin of the separating plane is m=d++d-.
Supose that the set of training points are linearly separable, ie, there
exists a plane wx+b=0 such that the points
xi with yi=1 ("positive" points)
lay on one side and those with yi=-1 ("negative" points)
on the other side.
w is the normal to the plane and
|b|/|w| is the distance of the origin from the plane.
Let d+ and d- be the shortest distances of the
positive and negative points, respectively, from the separating plane.
The margin of the separating plane is m=d++d-.
The support vector algorithm is the search for the plane parameters
(
b and
w) that maximizes the margin.
The constraints
| xi w + b |
≥ |
+1 |
for yi=+1 |
| xi w + b |
≤ |
-1 |
for yi=-1 |
can be formulated in a unified form,
y
i (
xi w + b ) ≥ 1
The margin turns out to be 2/|
w|. Therefore it is maximum when
teh norm of
w is minimum. This is a constrained minimum, which can
be formulated using Lagrangian multipliers a
i.
The Lagrangian
LP = 1/2 |w|2
- ∑ ai yi ( xi w + b )
+ ∑ ai
must be minimized with respect to
w,
b, requiring
dL
P/da
i = 0, and subject to the constraints
a
i ≥ 0 (because the original constraints are inequalities).
It is convenient to cast the problem in the dual form, by solving the
equations dLP/dw=0 and dLP/db=0. The dual
Lagrangian
LD = ∑ ai
- 1/2 ∑ ai aj yi yj
xi xj
must be maximized with respect to ai (in the subspace of
positive ai), subject to the constaint
(that derives from dLP/db=0)
∑ ai yi = 0
In the solution the point for which ai>0 are the "support
vectors" and lie on two planes (one "positive" one "negative") parallel
to the separating plane. The others lie on the respective sides of these
planes.
The solution to this problem is equivalent to the KKT
(Karush-Kuhn-Tucker) conditions (because it satifyes a certain technical
regularity condition),
| dLP/dw =
w - ∑ ai yi xi |
= |
0 |
| dLP/db = - ∑ ai yi |
= |
0 |
| yi ( xi w + b ) - 1 |
≥ |
0 |
| ai |
≥ |
0 |
| ai ( yi
( xi w + b ) - 1 ) |
= |
0 |
The normal to the plane
w is explicitly determined by the training set,
w = ∑ ai yi xi
therefore it is the weigthed sum over the support vector points.
The threshold
b is determined by the last of the KKT conditions.
In the test phase a point
x is assigned to the "positive" or to the
"negative" class depending on sgn(
w x + b ).
If the training points are not separable, we cannot find a separating
plane. We can relax the constraints allowing for some error,
y
i (
xi w + b ) ≥ 1 -
e
i,
and assign an extra cost for the errors, C(∑ e
i)
k,
in the objective function L
P.
This is a convex problem for any integer
k. When
k is 1 or 2
it is also a quadratic programming problem. If
k=1, furthermore
neither e
i, nor the associated multipliers appear in L
D.
LP =
1/2 |w|2 + C ∑ ei
- ∑ ai ( yi ( xi w + b )
- 1 + ei ) - ∑ ui ei
The KKT conditions are an extension of those for the separable case.
In particular we have also
| dLP/dei = C - ai - ui |
= |
0 |
| ei |
≥ |
0 |
| ei ui |
= |
0 |
Nonlinear Support Vector Machines
Suppose that the training points are mapped in a
(higher dimension) inner-product space,
F : Rn -> H
such that in this new space the problem becomes linear.
The training algorithm depends then on the kernel function
K(xi, xj) =
F(xi) F(xj).
The solution will give a vector w which is a weighted linear
combination of the support vectors F(xi).
Therefore the classification test is the sign of
∑ ai yi K(xi, x) + b
A necessary and sufficient condition for the existance of H and F
is the Mercer's condition:
for any g with finite L2 norm,
∫ K(x, y) g(x) g(y) dx dy
≥ 0
For example this condition is satisfied for positive integral powers of the
dot product.
[... to continue]
Marco Corvi - Page hosted by
geocities.com.
 Supose that the set of training points are linearly separable, ie, there
exists a plane wx+b=0 such that the points
xi with yi=1 ("positive" points)
lay on one side and those with yi=-1 ("negative" points)
on the other side.
w is the normal to the plane and
|b|/|w| is the distance of the origin from the plane.
Let d+ and d- be the shortest distances of the
positive and negative points, respectively, from the separating plane.
The margin of the separating plane is m=d++d-.
Supose that the set of training points are linearly separable, ie, there
exists a plane wx+b=0 such that the points
xi with yi=1 ("positive" points)
lay on one side and those with yi=-1 ("negative" points)
on the other side.
w is the normal to the plane and
|b|/|w| is the distance of the origin from the plane.
Let d+ and d- be the shortest distances of the
positive and negative points, respectively, from the separating plane.
The margin of the separating plane is m=d++d-.