N.B. This page is copied from http://blas.cis.mcmaster.ca/~monger/hsl-rgb.html

The conversion algorithms for these color spaces are originally from the book Fundamentals of Interactive Computer Graphics by Foley and van Dam (c 1982, Addison-Wesley). Chapter 17 describes color spaces and shows their relationships via easy-to-follow diagrams.

RGB - HSL

1. Convert the RBG values to the range 0-1
2. Find min and max values of R, B, G, say Xmin and Xmax
3. Let L = (Xmax + Xmin) / 2
4. If Xmax and Xmin are equal, S is defined to be 0, and H is undefined but in programs usually written as 0
5. Otherwise, test L:
   • If L < 1/2, S=(Xmax - Xmin)/(Xmax + Xmin)
   • Else, S=(Xmax - Xmin)/(2 - Xmax - Xmin)
6. Now find H:
   • If R=Xmax, H = (G-B)/(Xmax - Xmin)
   • If G=Xmax, H = 2 + (B-R)/(Xmax - Xmin)
   • If B=Xmax, H = 4 + (R-G)/(Xmax - Xmin)
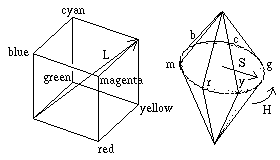
   If H < 0 set H = H + 6. Notice that H ranges from 0 to 6. RGB space is a cube, and HSL space is a double hexacone, where L is the principal diagonal of the RGB cube. Thus corners of the RGB cube; red, yellow, green, cyan, blue, and magenta, become the vertices of the HSL hexagon. Then the value 0-6 for H tells you which section of the hexgon you are in. H is most commonly given as in degrees, so to convert H = H*60.0 (If H is negative, add 360 to complete the conversion.)

HSL - RGB

1. If S=0, define R, G, and B all to L
2. Otherwise, test L:
   • If L < 1/2, temp2=L*(1+S)
   • Else, temp2=L+S - L*S
3. Let temp1 = 2 * L - temp2
4. Convert H to the range 0-1
5. For each of R, G, B, compute another temporary value, temp3, as follows:
   • for R, temp3=H+1/3; if temp3 > 1, temp3 = temp3 - 1
   • for G, temp3=H
   • for B, temp3=H-1/3; if temp3 < 0, temp3 = temp3 + 1
6. For each of R, G, B, do the following test:
   • If temp3 < 1/6, color=temp1+(temp2-temp1)*6*temp3
   • Else if temp3 < 1/2, color=temp2
   • Else if temp3 < 2/3, color=temp1+(temp2-temp1)*(2/3 - temp3)*6
   • Else color=temp1
7. Scale back to the range 0-255

Marco Corvi - Page hosted by geocities.com.